とりあえず、有限要素法で微分方程式が解けることは分かった。
でもこのままでは、数学の世界から出られないので、今回は静電場の支配方程式を考えます。
静電場を支配している法則は、ガウスの法則です。
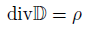
マクスウェル方程式のうちの一本であります。
標語的に言えば、「電荷密度から電束密度が発散する」とかそんな感じ。
電荷から、電気力線が四方八方に飛び出してるイメージです。
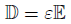
電束密度と電界の関係。
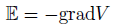
電界と電位の関係。
力と位置エネルギーの関係とよく似てます。
電磁気学の世界におけるポテンシャルは電位だから当然といえば当然。
これをぽいぽいっと、代入してみます。
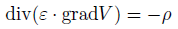
そろそろ体が拒否反応を示し始める頃です。
分かりやすくしよう。
ベクトル演算をナブラで表現します。
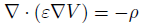
εは誘電率です。
これが式の中間に入ってますが、敢えて外には出してません。
それは、誘電率が等方性でない場合を考えてのことです。
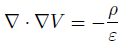
どちらの方向から見ても、誘電率が等しい場合。
つまり等方性の場合はただの定数にすぎないので、外に出せます。
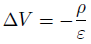
ナブラナブラはラプラシアンです。
そして完成したのは、ポアソン方程式です。
電気の世界でポアソン方程式といえば、これのこと。
つまりガウスの法則の特殊な場合です。
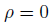
静電場で電荷がない場合という状況も少なくありません。
この場合は、式が更に簡単になります。
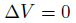
こちらはラプラス方程式という名前がついてます。
ラプラシアンに拒否反応の人のために、一次元バージョンも紹介します。
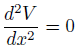
これなら簡単に解が求められますねー。
電位の2階微分が定数ということは、電位は線形な関数です。
抵抗に電圧を印加したときの電位分布をイメージしたら、納得できます。
以前、この3次元のラプラス方程式によって、抵抗を計算しました。
こちらも参考にしてください。
抵抗器のモデリング
実際に計算できると分かれば、マクスウェル方程式もやさしく思えます。
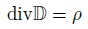


コメント