xとyの平均の点を通る直線。
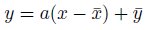
この傾きを統計学的に求めれば、それが回帰直線です。
では、いかに傾きを決定するか?
その数学的理由は後で述べるとして、結論から。
この傾きは、共分散と分散の比で決まります。
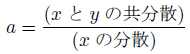
こんな具合。
分散は高校でも習った言葉だけど、共分散って何だ?
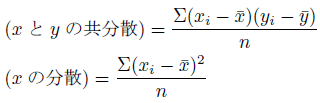
これが分散と共分散の定義。
こうやって見ると、xとxの共分散が、xの分散とも言えるような定義ですね。
分散はサンプルの広がり具合。
共分散は、xとyの相関の強さにも関係する指標です。
また別の指標ですが、「相関係数」というものは、共分散を分散で規格化したものです。
逆に言えば、共分散も相関係数に近い性質があるということです。
言葉で表現すると。
共分散は、「偏差積」、つまり「xの偏差とyの偏差の積」の平均。
分散は、「xの偏差の2乗」の平均。
そういうわけで、単回帰分析によって得られる回帰直線は以下。
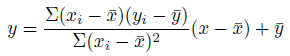
グラフも描いておきます。

プロットの真ん中を通っている感じはしますね。
次は、解析的に回帰直線を求めてみます。
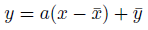

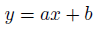
コメント
[…] 回帰直線を求める(2) 回帰直線を求める(3) […]