MOSFETの特性

今さらですが、MOSFETの特性について。
なんとびっくり、最近になってようやく動作が理解できたので。

MOSFETは、4端子素子です。
端子数の多さが、理解の難しさの原因だと思います。

抵抗器は2端子素子で、電圧の変数1つと電流の変数1つを考えれば十分。
対して4端子のMOSFETの場合は、電圧の変数が3つと、電流の変数3つを考える必要があります。

基板の端子を無視して3端子素子と考えれば、電圧の変数が2つと、電流の変数が2つ。
更に、ゲート端子に電流が流れないとすれば、電流の変数が1つになります。

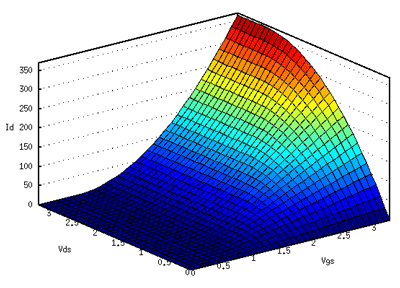
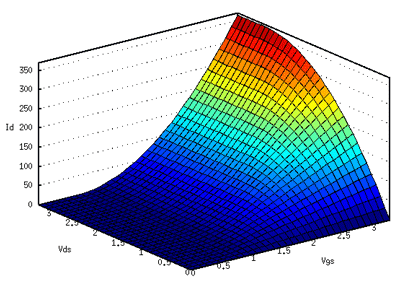
ここまでしてようやく、3次元のグラフで表現できます。
4変数以上になると、グラフ化は大変です。

教科書に、このグラフを載せてほしいんだよなー。
VgsかVdsを固定した場合の2次元のグラフなら、どの教科書にも載っているのだけど。

これをみると、平らな坂道(左のあたり)と、曲がった坂道(右のあたり)と、平地があります。
平らな坂道は「飽和領域」、曲がった坂道は「非飽和領域」と呼ばれます。
平地は、「弱反転領域」です。

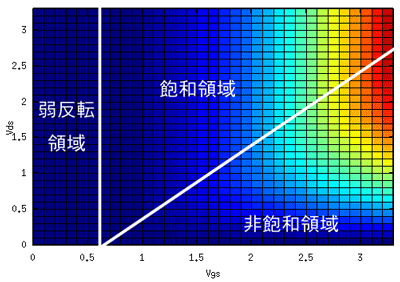
今のグラフを、「上」から見たものです。
したがって、横軸がVgs、縦軸がVdsです。
グラフのどのあたりが、どの領域に対応するかを確認です。

弱反転領域

飽和領域
V_{GS} – V_{TH}’); ?>

非飽和領域

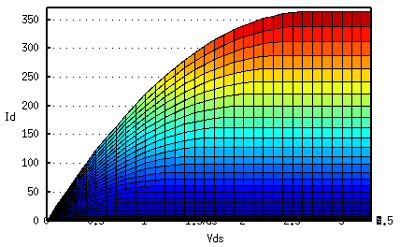
今度は、「左」から見たものです。
したがって、横軸がVds、縦軸がIdです。

Vdsを大きくすると、電流値が平らになります。
これが飽和領域。

このあたりで使えば電圧に対する電流の変動が小さいので、定電流源として使えます。

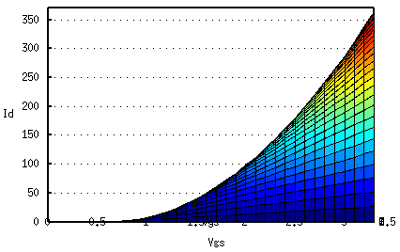
今度は、「右」から見たものです。
したがって、横軸がVgs、縦軸がVdsです。

Vgsが小さいあたりは、電流が流れない弱反転領域です。
厳密にはサブスレッショルドリークというのがあるのだけど、グラフに見えないくらいの微小電流です。

Vgsが大きい所は非飽和領域。

Vgsの変動が電流の大きな変動になるので、電圧増幅ができます。

4端子で考えなければならない基板バイアス効果については、まだ良く理解できてない。
へっぽこです。