なかなか面白い話題がありました。
「表皮効果」というやつです。
その前に「電磁気学の考え方」からの話題で、抵抗についてです。
オームの法則の比例定数である抵抗というやつ。
こいつは実験的に以下のように求められています。

注目すべきは分母のSです。
断面積が広いほど抵抗が小さくなる、というのは直感的に理解できます。
でも、これは実は予想外の実験結果だったのです。
というのも、静電的に導体に電荷を加えると、反発しあって電荷は導体の周囲だけに集まります。
周囲だけであって、全体にまんべんなく広がるなんてことはないのです。
というわけで当初の予想では、抵抗値は導線の周辺長に比例すると考えられていたのです。
これを始めに聞いたときは、「た、確かに!」と思ったものです。

このノートにこんな落書きがあったーり、なかったーり。
頑張りますよ。
そして、今読んでいる「デジタルシステム工学」から「表皮効果」です。
今度は逆に電流が導線の全体を通らないという話。
どういう場合にこの現象が起きるかといえば、高周波になったときです。

導線の中心ほど電流密度は小さくなるのです。
δは「表皮深さ」というもので、以下のように定められています。
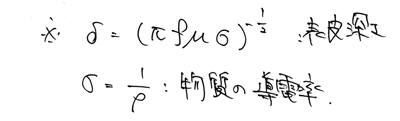
周波数fが上がるほど、表皮深さは浅くなり、電流は導線の周辺しか通らなくなります。
電流密度の積分をすれば抵抗が求められるわけですが、次のように近似して考えます。
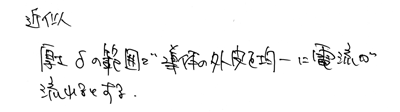
上の絵の斜線部分だけを電流が均一に流れるという近似ですね。
この斜線部分の面積、つまり電流が流れる面積を計算します。

下の方は自分の確認用です。
結局、次のように抵抗が求められます。
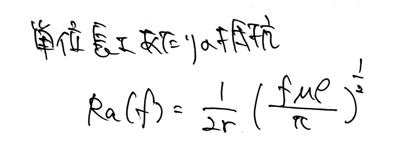
抵抗が周波数に依存していますね。
最後にどのくらいの周波数から、表皮効果を考える必要があるのか。

この式は上のδの定義から導出できます。
・・・という感じです。
抵抗が周波数に依存するなんて、またビックリだよねー。
高周波の回路っていうのは、どこまでも予想外の動きをしますね。



コメント